What causes an eclipse?
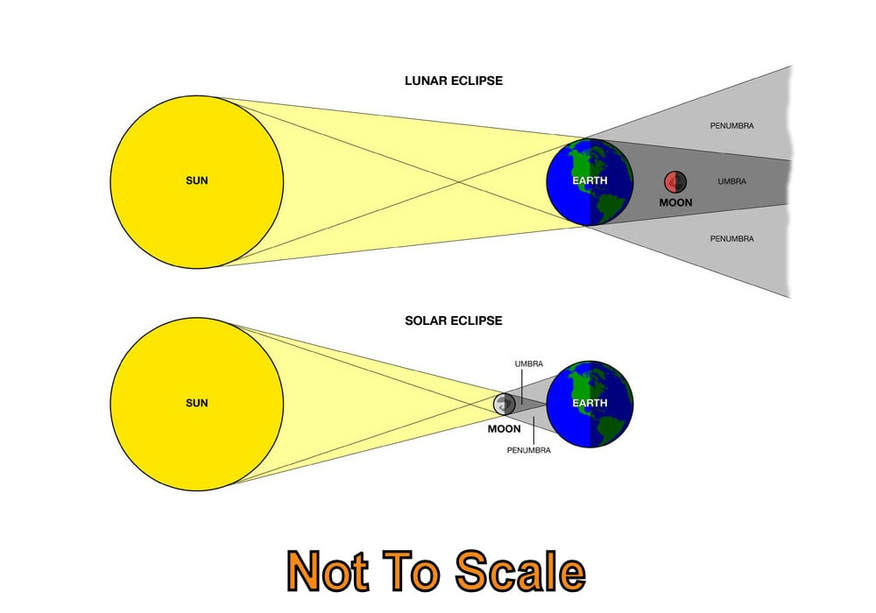
An eclipse is caused by the intersecting orbital paths of the Earth and Moon around the Sun. The geometry of the shadows cast by the Sun determines whether the eclipse is observed as a partial or total eclipse.
An eclipse is caused by the intersecting orbital paths of the Earth and Moon around the Sun. The geometry of the shadows cast by the Sun determines whether the eclipse is observed as a partial or total eclipse.
A lunar eclipse occurs when Moon's orbit around the Earth causes it to enter the shadow of the Earth at a full moon, directly opposite from the Sun. The eclipsed Moon can be observed anywhere from the Earth where it is night. When the entire full moon enters completely into the umbra – the fully shaded inner part of a shadow - it is termed a total lunar eclipse. However, the Earth's atmosphere scatters blue light more than red (and is why the sky is blue), and the thin ring of the Earth's atmosphere would show every sunset taking place around our planet, casting the Moon in varying shades of orange-red. Hence the origin of the overly dramatic term "blood moon":
January 31, 2018 Total Lunar Eclipse. Copyright Michael McKeag
A solar eclipse occurs at a new moon when, as the Moon orbits the Earth, its path crosses directly between the Earth and the Sun. Depending on the Moon’s distance from the Earth and its path in front of the Sun, a solar eclipse can be seen as total, annular, or partial. In a total solar eclipse the entire Sun is obscured by the Moon for anyone observing along the narrow path of the umbra - also know as the path of totality. A total solar eclipse - where the Moon completely hides the blinding disc of the Sun - is one of the rarest and most beautiful astronomical wonders a person can observe, revealing the ever-changing ephemeral corona - the Sun's outermost atmospshere. This is a once-in-a-lifetime event for most people – if they are lucky enough to witness a total solar eclipse at all:
|
|
August 21, 2017 total solar eclipse, near John Day Fossil Bed Sheep Rocks Unit, Oregon, USA. Copyright Mike McKeag.
|
|
Get thee to totality... and clear skies
While a partial solar eclipse is interesting, a total solar eclipse is mind-blowing. Most photo's can't do a total eclipse justice, and it's perhaps the most spectacular natural phenomena you will ever witness - "an experience of a lifetime." Indeed, people often travel the globe to be able to experience the magic that occurs ever so briefly during a total solar eclipse. So don't be fooled, seeing anything less than a 100% total eclipse can't compare - it's not even close. Why? The difference between a partial and total eclipse is quite literally the difference between day and night. The Sun is so incredibly bright that even one percent of the Sun still shining ruins everything - and you will not be able to see the Sun's outermost layer - the solar corona. To view the corona, you have to go into the path of totality - and as close to the center-line as possible for the longest duration of totality. If a total eclipse happens within a thousand miles of you, get in your car and go. You’ll remember it your whole life.
Partial solar eclipse
Total solar eclipse
The images below capture the intricate detail of the Sun's corona - which is visible only during totality. Although discernible to the eye, the subtle details and extreme ranges in the corona's brightness are notoriously difficult to photograph. These images are successful via the use of multiple exposures and sophisticated digital image processing. Clearly visible are intricate layers and glowing arcs and streamers of an ever changing mixture of million degree hot plasma and magnetic fields. Bright looping prominences appear pink just above the Sun's limb. Copyright Miloslav Druckmüller, Institute of Mathematics, Faculty of Mechanical Engineering Brno University of Technology, Czech Republic.
Detailed HDR View of a Solar Eclipse Corona, 2017, Miloslav Druckmüller, et.al.
|
|
The amazing appearance of the Sun's corona and chromosphere prominences seen through binoculars or a small telescope. 2008 total solar eclipse, Miloslav Druckmüller, Martin Dietzel, Peter Aniol, Vojtech Rušin, image processing by Miroslav Druckmüller.
|
|
Once you see a total solar eclipse the next words out of your mouth will be "When is the next one?"
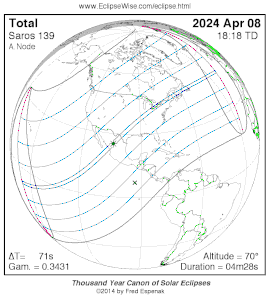
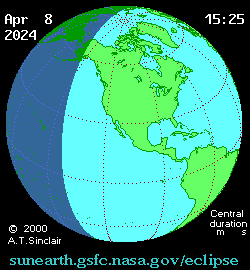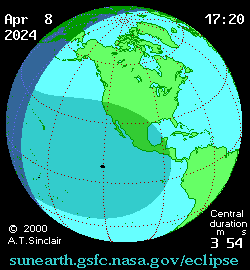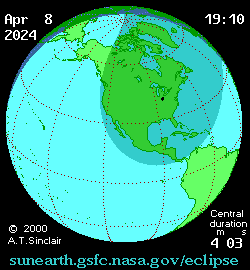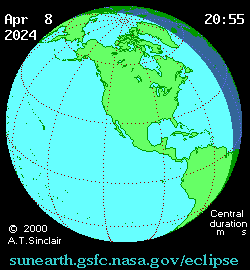
APRIL 8, 2024 Total Solar Eclipse
|
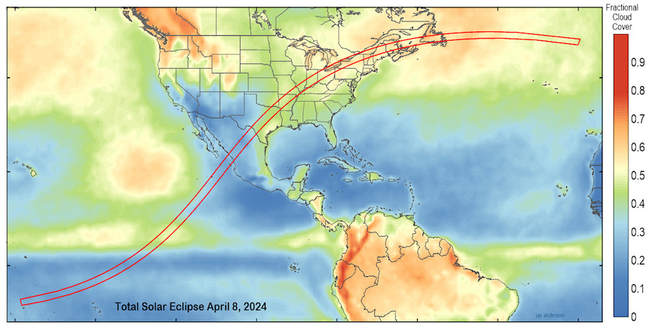
A total solar eclipse takes place somewhere on the Earth about every eighteen months, but are confined to a few fleeting moments along a narrow strip averaging about 60 to 100 miles (96 -160 km) wide, and are often located in remote or inhospitable regions of the planet. The total solar eclipse of Monday, April 8, 2024 will be the next total eclipse visible from the United States. Interactive 2024 eclipse map here. |
|
The weather in April for the path of totality in the USA is generally poorer than the 2017 total solar eclipse, which occurred in August. Weather prospects in April are best for Mexico and Texas, and the eclipse duration there will also be the longest at almost 4 1/2 minutes.
Historical cloud cover for April. Eclipsophile.com
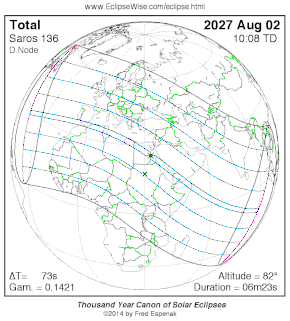
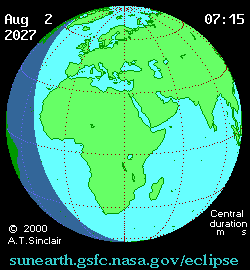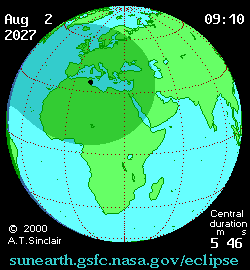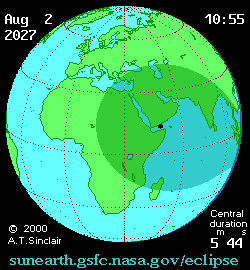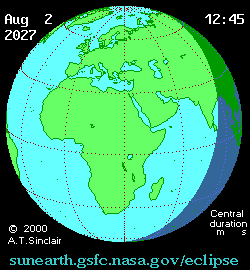
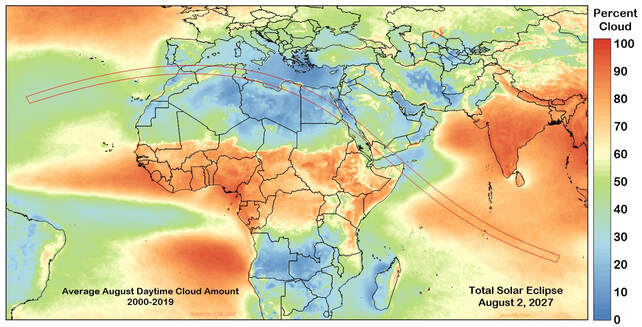
AUGUST 2, 2027 Total Solar Eclipse
|
For total solar eclipse aficionados, and those in search of an exotic (and sunny warm) location, should definitely consider traveling to Luxor Egypt for the August 2, 2027 total solar eclipse, where the prospect for the lack of clouds is obviously excellent. This is one of the longest total eclipses that can be seen - the Sun will be near aphelion (farthest away due to the Earth's elliptical orbit around the Sun), and thus much smaller than the Moon, which will be at perigee (closest to the Earth in its orbit) making for 6 minutes and 23 seconds of totality. |
|
Historical cloud cover for August. Eclipsophile.com
Interactive 2027 eclipse map here.
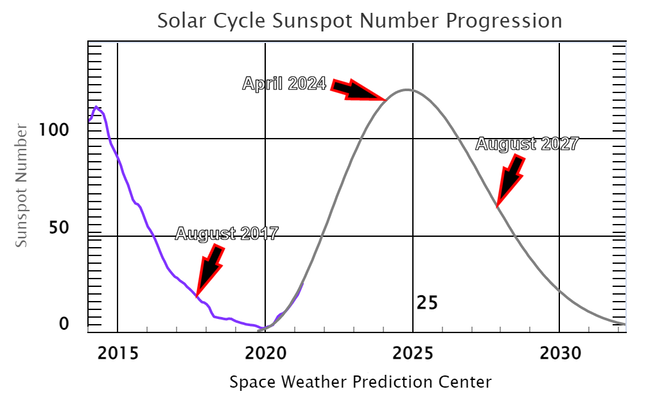
While it is difficult to predict the complexity of the solar corona's shape and features more that a month or two from the actual eclipse date, the fact that both the April 8, 2024 and August 2, 2027 total solar eclipses occur near the peak of sunspot cycle 25 could be promising for an even more spectacular coronal presentation than the August 21, 2017 eclipse (which as shown above was quite amazing in itself), which occurred near the sunspot minimum of cycle 24.
|
|
Streamers in the Sun's corona during a solar eclipse. In the left image, taken in 1994 near solar min, the streamers are mostly absent from the Sun's poles. In the right image, taken near solar max in 1980, streamers sprout from all solar latitudes.
|
|
Future solar eclipses detailed here.
Historical Note: The chances that you can see a total solar eclipse from any given single location in you lifetime is pretty remote. The mean frequency for a total eclipse of the Sun for any given point on the Earth's surface is once in 375 years. Given this, the fact that Goldendale Washington had a total solar eclipse in 1979, preceded by one only 61 years earlier in 1918, is quite amazing.
The 1918 total solar eclipse is of historical significance for Goldendale also because an eclipse expedition from Lick Observatory in California came to Goldendale to observe and photograph the eclipse. They hoped to get images to confirm Albert Einstein's theory that the intense gravity of the Sun would warp space and bend starlight enough to shift the positions of the stars in the sky. They also wanted to look for the postulated presence of another planet orbiting the Sun named "Vulcan" - way before Star Trek existed. Below you can see the expedition leaders along with support staff and friends from the local area standing in front of the "Einstein-Vulcan telescope."
Courtesy Special Collections, University Library, University of California Santa Cruz. Lick Observatory Records.
Goldendale will be lucky once again when a total solar eclipse occurs more frequently than average for a given location on June 24, 2169 - a mere 190 years after the 1979 total solar eclipse seen in the town.
